中枢网关的代数怎么看？

在复杂多变的网络架构中，中枢网关扮演着至关重要的角色，它负责调度数据流、确保网络通信的高效与稳定。而要深入了解中枢网关的工作原理，我们必须借助一些数学工具，其中代数便是不可或缺的一环。本文将带领您从代数的角度解读中枢网关，探索其背后的数学原理，并提供实用的解读方法。

一、中枢网关与数学的关系

中枢网关作为网络架构中的核心设备，其工作原理涉及到路由选择、数据包转发等多个层面。数学，尤其是代数，为理解和设计这些功能提供了理论基础。代数中的方程式和矩阵运算等工具，能够帮助我们更精确地模拟网络流量和处理网络请求。

二、代数在网络中的应用

网络工程师在设计和优化中枢网关时，会用到代数中的哪些概念呢？下面是几个关键点：

1.线性代数与矩阵运算

矩阵运算是线性代数的重要组成部分，它在路由算法中被广泛应用。通过矩阵运算，可以表达和处理网络流量的分配问题，确定数据包在不同网络节点之间的最短路径，即用矩阵表示网络拓扑结构，并通过算法求解。

2.逻辑代数在网络协议中的应用

逻辑代数，特别是布尔代数，是分析和设计网络协议的基础。它使用逻辑运算符（如AND、OR和NOT）来描述网络设备的行为规则，访问控制列表（ACL）的配置，就是基于布尔逻辑的。

3.图论与网络拓扑

图论是研究图的数学理论和方法，网络拓扑可以被视为一个图，其中的节点代表网络设备，边代表它们之间的连接。在设计网络时，图论提供了一套工具来分析网络的连通性、冗余度和其它关键属性。

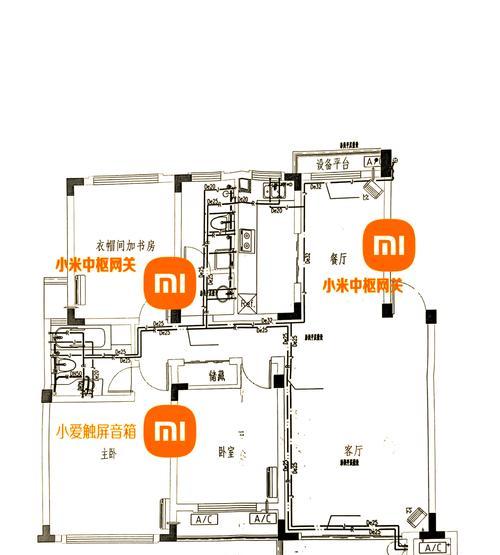
三、解读中枢网关的代数过程

我们以一个简单的例子来说明如何使用代数工具来分析中枢网关的工作原理：

1.确定网络模型

我们需要建立网络模型。这个模型可能包含多个路由器、交换机和终端设备，并用矩阵来表示它们之间的连接关系。

2.利用代数方程表达网络流量

接下来，我们利用代数方程来模拟网络中的流量。这些方程基于网络模型，考虑了各节点的连接权重、数据包的大小和数量等因素。

3.解决方程求解最优路径

通过解这些代数方程，我们可以找到网络中的最优路径。在实际操作中，这通常需要运用计算机算法来高效完成，如最短路径算法（Dijkstra算法）或贝尔曼-福特算法（Bellman-Fordalgorithm）。

四、实际应用中的挑战与解决方案

在实际应用中，中枢网关的设计和优化面临许多挑战，比如网络环境的动态变化、流量的不均匀分布等。为了应对这些挑战，我们可以采用以下策略：

1.动态路由算法

通过引入动态路由算法，网络设备能够根据实时数据流来动态调整路由策略，从而保证网络的高效运行。

2.机器学习辅助优化

借助机器学习模型，可以预测网络流量的模式，提前作出路由决策，减少拥塞和延迟。

五、与展望

综合以上内容，我们可以看到代数在中枢网关设计与优化中的关键作用。从线性代数到图论，再到逻辑代数，代数工具帮助我们以精确的方式理解和控制网络的复杂性。随着技术的进步，代数模型和算法将与机器学习、人工智能等更先进的技术融合，进一步提升中枢网关乃至整个网络架构的性能和智能化水平。